August 15, 2023

Natural numbers

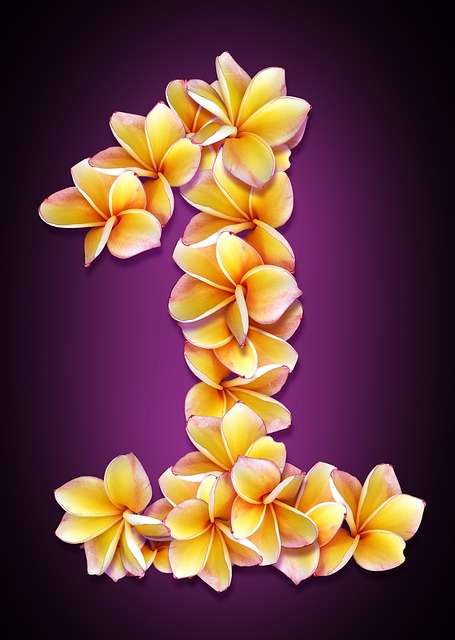
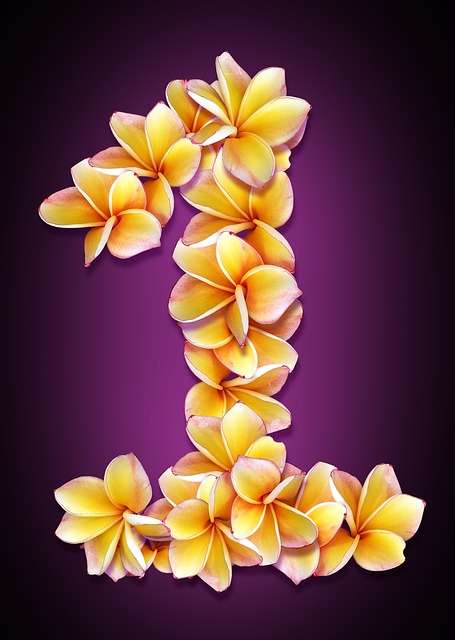
Natural numbers, often referred to as counting numbers, are the set of positive integers starting from 1 and continuing infinitely: 1, 2, 3, 4, 5, and so on. In mathematical notation, the set of natural numbers is often denoted as ℕ.

These numbers are used for counting and ordering, and they are fundamental in various mathematical operations and concepts. Natural numbers are also the basis for other sets of numbers, such as whole numbers, integers, rational numbers, and real numbers.

Natural Numbers (ℕ):

The positive integers that start from 1 and continue indefinitely.

Whole Numbers (ℤ⁺):

The set of non-negative integers, including 0: 0, 1, 2, 3, and so on.

Integers (ℤ):

The set of positive and negative whole numbers, including 0: ..., -3, -2, -1, 0, 1, 2, 3, ...

Rational Numbers (ℚ):

Numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. Examples include 1/2, -3/4, 2, and -5.

Real Numbers (ℝ):

The set of all numbers on the real number line, including both rational and irrational numbers. Irrational numbers cannot be expressed as fractions and have non-repeating decimal expansions, such as π (pi) and √2 (square root of 2).

Natural numbers are a fundamental concept in mathematics and have applications in various fields, including arithmetic, algebra, number theory, and more.